Image credit: Hyungjin ChungAbstract
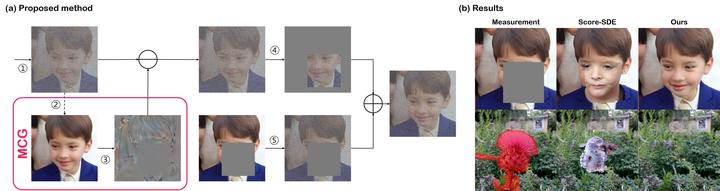
Recently, diffusion models have been used to solve various inverse problems in an unsupervised manner with appropriate modifications to the sampling process. However, the current solvers, which recursively apply a reverse diffusion step followed by a projection-based measurement consistency step, often produce sub-optimal results. By studying the generative sampling path, here we show that current solvers throw the sample path off the data manifold, and hence the error accumulates. To address this, we propose an additional correction term inspired by the manifold constraint, which can be used synergistically with the previous solvers to make the iterations close to the manifold. The proposed manifold constraint is straightforward to implement within a few lines of code, yet boosts the performance by a surprisingly large margin. With extensive experiments, we show that our method is superior to the previous methods both theoretically and empirically, producing promising results in many applications such as image inpainting, colorization, and sparse-view computed tomography.
Hyungjin Chung
Ph.D. student - Generative Models & Inverse Problems
My research interests include, but is not restricted to developing efficient, modular deep generative models (diffusion models), and solving real-world inverse problems (MRI, tomography, microscopy, phase retrieval, etc.) with deep generative priors.