Image credit: Hyungjin ChungAbstract
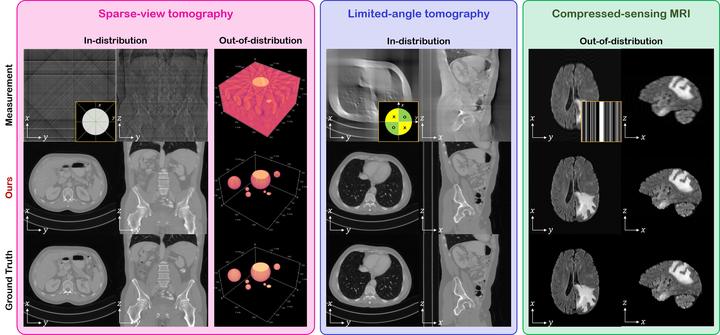
Diffusion models have emerged as the new state-of-the-art generative model with high quality samples, with intriguing properties such as mode coverage and high flexibility. They have also been shown to be effective inverse problem solvers, acting as the prior of the distribution, while the information of the forward model can be granted at the sampling stage. Nonetheless, as the generative process remains in the same high dimensional (i.e. identical to data dimension) space, the models have not been extended to 3D inverse problems due to the extremely high memory and computational cost. In this paper, we combine the ideas from the conventional model-based iterative reconstruction with the modern diffusion models, which leads to a highly effective method for solving 3D medical image reconstruction tasks such as sparse-view tomography, limited angle tomography, compressed sensing MRI from pre-trained 2D diffusion models. In essence, we propose to augment the 2D diffusion prior with a model-based prior in the remaining direction at test time, such that one can achieve coherent reconstructions across all dimensions. Our method can be run in a single commodity GPU, and establishes the new state-of-the-art, showing that the proposed method can perform reconstructions of high fidelity and accuracy even in the most extreme cases (e.g. 2-view 3D tomography). We further reveal that the generalization capacity of the proposed method is surprisingly high, and can be used to reconstruct volumes that are entirely different from the training dataset.
Hyungjin Chung
Ph.D. student - Generative Models & Inverse Problems
My research interests include, but is not restricted to developing efficient, modular deep generative models (diffusion models), and solving real-world inverse problems (MRI, tomography, microscopy, phase retrieval, etc.) with deep generative priors.